May 2024
Welcome to EFM's May Newsletter!
It is essential that every caregiver in the world reads books and does math with their young children!
EFM believes in every child’s mathematical right to equity, opportunity, and personal fulfillment.
News
EFM Playing Cards and Storybooks – A big shipment of EFM playing cards and storybooks has arrived in the US! Please go to the EFM ordering page, or write to me, if you are interested in getting some of these materials.
Number Theory for Preschoolers
The mathematician Carl Friedrich Gauss said “Mathematics is the queen of the sciences and Number Theory is the queen of Mathematics.” Young children can access a surprisingly large amount of the beautiful world of number theory. When this is approached with a sense of wonder and discovery, it can lead to a lifelong love of numbers.
At its heart, Number Theory is about how numbers fit together and interrelate. When children consider how to group things to count them, why some numbers of things can be split evenly in two, or why some pairs of numbers create interesting patterns when going around a circle, they are playing with Number Theory.
Breaking Numbers Into Pieces – Counting Dots, Subitizing, Number Bonds, and Part / Whole
Taking a cluster of dots and exploring different ways to count them is a journey into Number Theory. I briefly explored the topic of subitizing in the June, 2023, newsletter and used the following illustration there.
Discussing your child’s ideas for counting the 17, 11, or 15 dots in these diagrams not only develops your child’s sense of quantities, it also is a lovely way to see how numbers are put together. The leftmost diagram can be three rows of five plus two more, or it can be five rows of five with four pairs taken out, or it can be any way your child wants to see it – all are good ways to see and think about 17.
Next is a graphic of Montessori counting rods from the November, 2023 newsletter. This shows all the number bonds for seven. Seeing and understanding all these ways of creating seven is a simple and lovely piece of Number Theory.
Number Shapes
Which shapes can you make with some number of markers? This question can lead to discussions and investigations for children at all levels, and it is a natural outgrowth of the subitizing discussions from the last section.
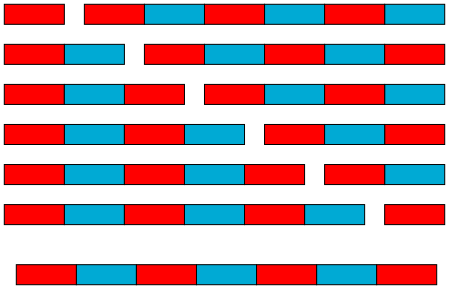
If you have some number of markers, say 7 or 8, when can you split them evenly into two matched rows? This is a natural entry point to a discussion of even and odd numbers without ever mentioning division by 2. Notice how the even and odd numbers are interlaced as you count, and how, for a given group, the numbers progress by 2’s – for example, odd numbers are 1, 3, 5, 7.
After you have played with that for a while, you can take these row representations and see how they combine. Why is that when you combine an even and an odd number, say 6 and 5 (as in the bottom illustration), you always end up with an odd number? You don’t need an algebraic proof to understand this rule about even and odd numbers, you can see it right there!
You can ask about all the rectangles you can make with some number of dots. Why do some numbers only have flat rectangles? This is a great way to introduce the idea of primes. Why do some numbers, such as 4, 9, and 25, only have three rectangles (two flat and one square)? These numbers are the squares of primes. What happens for numbers that have four rectangles (these are the cubes of primes and products of two primes)? This quickly gets too advanced for a very little child, but look at all the possibilities for growth as they get older!
What are the numbers that can be made into trapezoids? These are also called Staircase Numbers. For odd numbers greater than one, why are they always two-level staircase numbers? The answer to that is immediate from their earlier experiences with even and odd numbers.
What happens with three-level staircase numbers, such as 1 + 2 + 3 = 6 and 2 + 3 + 4 = 9? Why do you get all multiples of 3 greater than 3 this way? Describe what you can about other sizes of multi-level staircase numbers. Which numbers can never be staircase numbers? There is so much fun Number Theory going on!
Counting in Circles
There are beautiful designs to be made just by counting around a circle, and these designs reflect some basic number theory about how numbers share their factors. Your child can enjoy these designs without any understanding of divisibility and factors. However, as their understanding grows, these designs are ripe for exploration and understanding.
When there are 8 points (0 to 7), connecting the numbers that are every 1, 3, 5, or 7 creates one continuous design, but the other numbers have two or more pieces? For 9 points (0 to 8), why do 1, 2, 4, 5, 7, and 8 create a continuous design, but not 3, and 6? There’s lots to play with here.
Fibonacci Numbers
These numbers are created by starting with 0 and 1, and then adding together pairs of consecutive numbers. This produces the famous sequence 0, 1, 1, 2, 3, 5, 8, 13, and so on. There are a great number of sophisticated properties of this sequence, but there are also some very simple ones.
Perhaps the simplest is that pinecones and pineapples have the sequence built into them! Amaze your child by picking up one of these and coloring in the diagonal elements. Rather than my producing a mediocre graphic, go to the web and search for “pineapples and Fibonacci Numbers” or “pinecones and Fibonacci Numbers” to see some quite surprising drawings of how consecutive Fibonacci Numbers show up in nature.
There is a nice connection with the Golden Ratio and decomposing a rectangle into squares, something the ancient Greeks loved to do. For an example, use an 8 by 13 rectangle. When you remove an 8 by 8 square from one side of this, you are left with a 5 by 8 rectangles. When you remove a 5 by 5 square from this, you have a 3 by 5 rectangle, and so on. Each of these pairs of side lengths is a pair of consecutive Fibonacci Numbers. The larger the pair of numbers used, the closer their ratio is to the Golden Ratio!
Decomposing Numbers
How many ways can you add up to a number? There are many ways to ask this question, and some have interesting answers that are understandable to a child learning addition.
Suppose we ask how many ways there are to add up to a number and the order is important. There is 1 way to get 1, there are 2 ways to get 2 (1 + 1 and 2), there are 4 ways to get 3 (1 + 1 + 1, 2 + 1, 1 + 2, and 3), and so on. Each time, the number of ways doubles! Why is that?
Suppose we ask how many ways there are to add up to a number if we only use the numbers 1 and 2. There is 1 way to get 1, there are 2 ways to get 2 (1 + 1 and 2), there are 3 ways to get 3 (1 + 1 + 1, 2 + 1, and 1 + 2), there are 5 ways to get 4 (1 + 1 + 1 + 1, 2 + 1 + 1, 1 + 2 + 1, 1 + 1 + 2, and 2 + 2), and so on. These are the Fibonacci Numbers! Why do they show up here?
Wrapping Up Number Theory is a fun playground for a young child, and I hope I’ve opened the door for you to enter this playground together. Next month we’ll continue this theme by talking about Topology for Preschoolers.
If you have any questions or comments, please send them our way! We would enjoy the opportunity to chat with you. Also, if you are interested in collaborating with us or supporting us in any fashion, we would love to talk with you about ways we can work together!
May 18, 2024
Chris Wright
Chris@EarlyFamilyMath.org
Twitter | Facebook | Instagram
Early Family Math is a California 501(c)(3) nonprofit corporation, #87-4441486.