July 2024
Welcome to EFM's July Newsletter!
It is essential that every caregiver in the world reads books and does math with their young children!
EFM believes in every child’s mathematical right to equity, opportunity, and personal fulfillment.
News
Professional Development – A large school district in Canada contacted EFM about doing PD presentations. If having an EFM PD is of interest to you, let’s set something up [link]. Generally speaking, if you are willing to pay travel expenses and give feedback on EFM materials, I am happy to come to your district and do presentations and workshops. I have two topics all set to go: one on playful learning in the classroom and at home, and a second on problem exploration in the classroom.
Topology for Preschoolers – Part II
Last month I wrote about ways you and your child can play with the topology of curves. This month I want to go one dimension higher and explore how you can play with two-dimensional surfaces.
To review, Topology is all about understanding and describing shapes. If you have two very different looking shapes, such as a ball and an inner tube, how can you tell if they are the same? What does it even mean for them to be the same?
Topology usually considers two things the same if you can smoothly bend, stretch, or squash one to become the other. The standard example is that a teacup is the same as a donut. If you think of the teacup as made of clay, you can smoothly deform and squash the bowl of the cup until the teacup is just a handle. At that point, you have a donut!
Surfaces
Surfaces are spaces that, if you were a very small bug on the surface, what the bug would see would look like part of a piece of paper (think Flat-Earthers). Some surfaces have an edge, such as a piece of paper, and others do not, such as a sphere (a ball).
Möbius strip
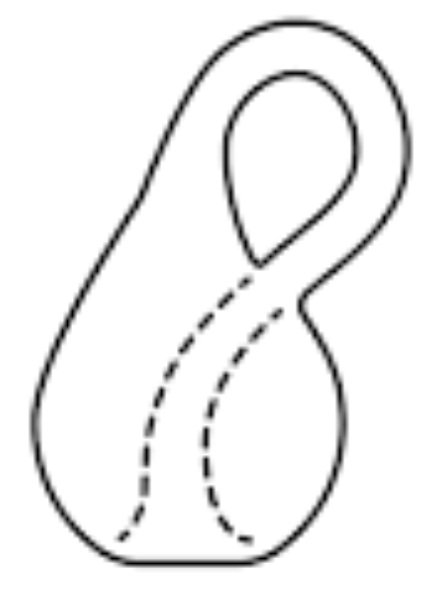
One popular surface to play with is a Möbius strip. Make one by taking a moderately narrow strip of paper, giving it a half twist, and then attaching the two ends together (with glue, tape, or staples).
The first thing to notice is that this strip has just one side. If you start at one point and travel around the surface, you can smoothly travel to any other point anywhere on the surface (without going over the edge).
Another aspect to explore is what happens when you cut the strip down the middle all the way around. Normally when you cut something down the middle, you get two pieces that look the same. Have your child predict what will happen before you do it.
Next, see what happens when you take the result of the cut you just made and cut that down the middle – were you surprised again? Another experiment is to make a line all the way around that is one-third of the way away from the edge and then cut along that line. What is the prediction this time?
Making Polyhedra with Nets
“Poly” means many. Polygons are objects with many sides, and polyhedra are objects with many faces. You can copy “nets” (which are available all over the web) to trace patterns on stiff paper to cut out and create many interesting polyhedra. Not only is this an interesting construction project, but once the models are done you will have physical tetrahedrons, cubes, octahedrons, and many other interesting shapes for your children to look at and think about.
One experiment to do with these polyhedra is to calculate the Euler Number. Add the number of faces to the number of corners, and then subtract the number of edges. You should always get the number 2! For example, for a cube this is (6 + 8) – 12 = 2. This number is the Euler Number for a sphere, and this number varies from surface to surface (if you do a similar experiment on a torus you will get a different answer).
Making Surfaces with Polygons
Similar to what was done with the Möbius strip, you can glue the edges of a polygon together to form various surfaces. In most cases, this is more theoretical than it is practical (in that many of the “glueings” are not possible to do with real life materials). None the less, they make for good thought experiments and some good games.
Use paper
If you take a sheet of paper and glue together opposite sides in the natural way, you will get a cylinder. This is a surface with two separate circles for its edge. If you take a sheet of paper, twist it, and glue together opposite sides, you will get a Möbius strip. This is a surface with just one circle for its edge.
If you take the cylinder you made earlier and glue together its opposite ends, you will get a torus (an inner tube or the surface of a donut). If instead you take the cylinder and glue together its opposite ends “inside out” you will get a Klein Bottle. Here is an artists drawing of what a Klein bottle would look like if it could exist in three dimensions (which it can’t).
A computer model is more fun
To help this come to life for your child, the site www.geometrygames.org has a collection of familiar games that can be played on surfaces. Go to their “Torus Games” section and see how things change on a torus or Klein Bottle when you play Tic-Tac-Toe, put together a jigsaw puzzle, or go through a maze.
Tilings
Playing with pattern blocks to make patterns and tilings is a classic children’s activity. You can find interesting patterns of tilings all around you in urban spaces. Your child will learn a lot while fitting the polygons together to see what works and what doesn’t.
Regular tilings are ones in which only one kind of regular (all edges and angles are the same) polygon is used. Here are the three regular tilings using a triangle, square, and hexagon. I have included an attempt to use pentagons to show how the angles don’t work out.
There are eight semi-regular tilings, which are illustrated below. For both regular and semi-regular tilings, the view from any vertex looks exactly the same. It is an interesting investigation for an older child to see why these 11 tilings are the only possible ones with this property.
Another interesting tiling playground is to play with aperiodic tilings. In particular, using Penrose tiles can be a lot of fun. The great thing about pieces that force aperiodic tilings is that your child won’t get stuck just reproducing the same pattern over and over.
Map Coloring
When a map maker colors a map, they use different colors for regions that share a border. A natural mathematical question that arises is: How many colors do you need for a given map? In 1976, it was finally proven that four colors suffice for any normal flat map (normal refers to requiring all regions to be made of one piece).
The Four Color Theorem and its proof are pretty abstract, but you and your child can have a lot of concrete fun coloring various types of maps.
2-colorable maps
Challenge your child to use just two colors to color in a map such as this one (not including the outside).
Any map that is created by adding a sequence of lines (straight or curved) can be colored using two colors. Here is a sequence of illustrations to show why that is true. Every time you add a new line, just flip all the colors on one side of the line to make it all work out.
It is tempting to conjecture that any map is two-colorable if all of its nodes (corners) have an even number of regions touching it. Check this out with your child.
3-colorable maps
If a map has a region that has an odd number of regions sharing sides with it, this map will require four colors. Why is that? In the map of US, Nevada has five states bordering it, so the US map requires 4 colors. It is tempting to conjecture that if all regions have an even number of neighbors, then the map is 3-colorable – is it true?
Coloring regular and semi-regular tilings
Look back at the 11 tilings shown earlier. How many colors are required for each of them?
Coloring maps on other surfaces
Things change for maps on a torus or other exotic surfaces. For a torus, a map can require as many as 7 colors! On a Möbius strip you can need up to 6 colors! Have fun creating maps on these surfaces and seeing how many colors each map takes.
Wrapping Up The topology of shapes is a natural playground for a young child. Next month I will continue this tour of advanced math topics that can be made simple, engaging, and fun for young children.
If you have any questions or comments, please send them our way! We would enjoy the opportunity to chat with you. Also, if you are interested in collaborating with us or supporting us in any fashion, we would love to talk with you about ways we can work together!
July 18, 2024
Chris Wright
Chris@EarlyFamilyMath.org
Twitter | Facebook | Instagram
Early Family Math is a California 501(c)(3) nonprofit corporation, #87-4441486.